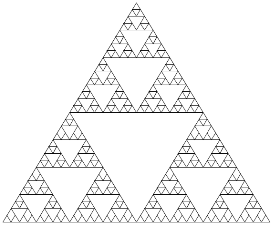
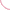| Фракталы
В сети опубликовали первый небольшой трехмерный мультфильм, который был полностью сгенерированный компьютером без вмешательства человека. https://sploid.gizmodo.com/this-captivating-sci-fi-short-film-was-randomly-generat-1820115896
Как отмечается, короткий 3D-мультфильм Fraktaal образовался исключительно автоматически сгенерированными фрактальными шаблонами. «Можно подумать, что я создатель короткометражного мультфильма - долго моделировал и рисовал его. Но так получилось, что я - ленивый мультипликатор и поэтому Fraktaal был сгенерирован фрактальными паттернами, с помощью которых и появились эти чужие миры и города », - признался голландский художник Джулиус Хорстуис, автор математических алгоритмов, которые использовал компьютер. https://player.vimeo.com/video/240563157
Джулиус Хорстуис и раньше использовал фракталы в компьютерной анимации, но на этот раз он доверил творчество компьютеру, который использовал созданные им математические и алгоритмы, выдавали рандомно данные на экран. «Благодаря фракталам я могу творить целые миры, и мне не нужно что-то рисовать или моделировать. Эти формы скрываются в формулах, они существуют в математической реальности, а мне нужно только исследовать и заставить их показать себя », - отметил художник.
К слову, фракталы - это нерегулярные, самоподобные структуры: фигуры, малые части которых в произвольном увеличении подобны ей самой. Термин «фрактал» ввел в 1975 году французско-американский атематик, основатель фрактальной геометрии Бенуа Мандельброт
- Геометрические фракталы применяются для получения изображений деревьев, кустов, береговых линий и тому подобное.
- Алгебраические и стохастические - для построения ландшафтов, поверхности морей, биологических моделей и других объектов.
Объекты, которые теперь называются фракталами, исследовались задолго до того, как им было дано такое название. В этноматематике, например в работах Рона Еглаша «Африканские Фракталы», задокументировано распространены фрактальные геометрические фигуры в искусстве туземцев. В 1525 году немецкий художник Альбрехт Дюрер опубликовал свой труд «Руководство Художника», один из разделов которой называется «Черепичные шаблоны, созданные пентагонами» (греч., от pente пять, и gonia угол- геометрическая фигура, окруженная 5- ю сторонами и 5- ю углами: пятиугольник). Американский художник-абстракционист Джексон Поллок рисовал объекты, очень похожие на фракталы.
Фракталы. Построение.
источник: сайт "ДистОсвiта",Оксана Пасичник:
https://dystosvita.gnomio.com/mod/page/view.php?id=2332
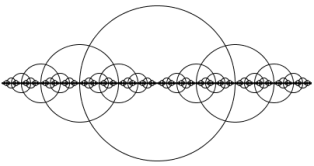
Пример 1.Рекурсивные круги
void setup() {
size(400,400);
smooth();
}
void draw() {
background(255);
stroke(0);
noFill();
drawCircle(width/2,height/2,200);
}
void drawCircle(float x, float y, float radius) {
ellipse(x, y, radius, radius);
if(radius > 2) {
drawCircle(x + radius/2, y, radius/2);
drawCircle(x- radius/2, y, radius/2);
}
}
|
|
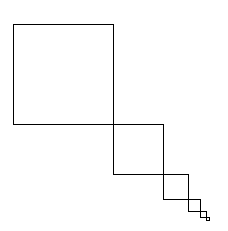
Пример 2. Рекурсивные квадраты
|
void setup() {
size(400,400);
smooth();
}
void draw() {
background(255);
stroke(0);
noFill();
kvadrat(100,100,100);
}
void kvadrat(int x, int y, int n)
{
if (n>1)
{
int x2=x+n;
int y2=y+n;
rect(x,y,n,n);
n=int(n/2);
kvadrat(x2,y2,n);
}
}
|
|
|
void setup() {
size(400,400);
smooth();//«включает» режим сглаженного рисования
}
void draw() {
background(255);
stroke(0);
noFill();
kvadrat(100,100,100);
}
void kvadrat(int x, int y, int n)
{
if (n>1)
{
int x2=x+n;
int y2=y+n;
stroke (0,0,255); //цвет контура
strokeWeight(2); //Толщина кисти (контура фигуры)
fill(0);
rect(x,y,n,n);// функция rect(x,y,width,height) - рисует прямоугольник
n=int(n/2);
kvadrat(x2,y2,n);
}
}
|
 |
Задание.Повернуть квадраты вверх и продолжить вниз:
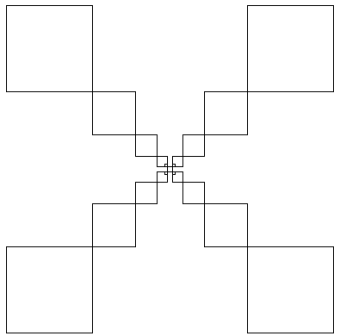
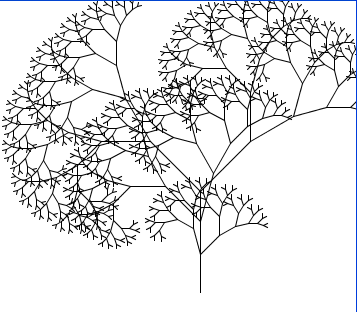
Пример 3. Фрактальные деревья
|
void setup() {
size(400,400);
smooth();//«включает» режим сглаженного рисования
}
void draw() {
background(255);
stroke(0);
noFill();
fract(mouseX,mouseY,int(random(100))+20,PI/2);
fract2(mouseX,mouseY,int(random(100))+20,PI/2);
fract3(mouseX,mouseY,int(random(100))+20,PI/2);
}
void fract(int x, int y, float l, float u){
if (l>5) {
l = l * 0.7;
line(x,y,round(x+l*cos(u)),round(y-l*sin(u)));
x = round(x + l * cos(u));
y = round(y - l * sin(u));
fract(x, y, l, u + PI / 4);
fract(x, y, l, u - PI / 12); }
}
void fract2(int x, int y, float l, float u){
if (l>5) {
l = l * 0.7;
line(x,y,round(x+l*cos(u)),round(y-l*sin(u)));
x = round(x + l * cos(u));
y = round(y - l * sin(u));
fract(x, y, l, u + PI / 12);
fract(x, y, l, u - PI / 4); }
}
void fract3(int x, int y, float l, float u){
if (l>5) {
l = l * 0.95;
line(x,y,round(x+l*cos(u)),round(y-l*sin(u)));
x = round(x + l * cos(u));
y = round(y - l * sin(u));
fract(x, y, l, u + PI / 4);
fract(x, y, l, u - PI / 4); }
}
|
 |
Пример 4. Треугольник Сперанского
|
void setup() {
size(640,500);
smooth();//«включает» режим сглаженного рисования
}
void draw() {
background(255);
stroke(0);
noFill();
int iter=5;
tr(320,10,600,470,40,470);
dr(320,10,600,470,40,470,iter);
}
void tr(float x1, float y1, float x2, float y2, float x3, float y3)
{
line(int(x1), int(y1), int(x2), int(y2));
line(int(x2), int(y2), int(x3), int(y3));
line(int(x3), int(y3), int(x1), int(y1));
}
void dr(float x1, float y1, float x2, float y2, float x3, float y3, int n)
{
if (n>0) {
float x1n = (x1 + x2) / 2;
float y1n = (y1 + y2) / 2;
float x2n = (x2 + x3) / 2;
float y2n = (y2 + y3) / 2;
float x3n = (x3 + x1) / 2;
float y3n = (y3 + y1) / 2;
tr(x1n, y1n, x2n, y2n, x3n, y3n);
dr(x1, y1, x1n, y1n, x3n, y3n, n - 1);
dr(x2, y2, x1n, y1n, x2n, y2n, n - 1);
dr(x3, y3, x2n, y2n, x3n, y3n, n - 1);
}
}
|
|
| |
