Высказывания. Логические константы. Логические операции

Для  решения  большинства  задач  линейных алгоритмов  недостаточно.  В  проектах,  которые  реализуют  другие  виды  алгоритмов,  например  алгоритмы  с  ветвлениями,  используют  логические  выражения. Рассмотрим логические выражения и операции над ними.

Логика (греч. logos -  слово, смысл, мысль, язык) - наука о формах, методах  и  законах  интеллектуальной  познавательной  деятельности,  правильного мышления, о способах рассуждений.

Один  из  разделов  логики  -  математическая  логика  -  является  наукой о  законах  математического  мышления.  К  основным  понятиям  математической  логики  относится  понятие  высказывание.  Под  высказыванием  понимают  повествовательное  предложение,  о  котором  можно  однозначно сказать,  правильное  (истинное)  оно  или  неправильное  (ложное).  Высказывания  обозначают  большими  буквами  английского  алфавита,  например:

А = «Киев - столица Украины», В = «2 + 2 = 5».

Основным  свойством  высказывания  является  его  истинность,  другие свойства  считаются  несущественными.  Значения  истинности  высказывания  обозначают  1  или  true,  если  высказывание  истинно,  О  или  false,  если высказывание  ложно.

 Например:

•  высказывание  А =  «Киев  -  столица Украины» является  истинным,  то  есть  значение  его  свойства  истинность равно  true;
• высказывание  С  =  «3  >  5»  является  ложным,  то  есть  значение его свойства истинность равно false.

Значения true и false называются логическими константами.

Из  заданных  высказываний  можно  получить  новые  -  составные,  используя  логические  операции:

• отрицание, 
• конъюнкцию  (лат.  conjunctio  -объединение),
• дизъюнкцию (лат. disjunctio -разъединение) и др.

Таблицы истинности.

Для определения результатов выполнения логических операций в математической логике используют таблицы истинности. В таблице истинности для каждого  возможного  набора  значений  свойства  истинность  высказываний приводится соответствующее значение этого свойства для высказывания, которое является результатом выполнения логической операции над ними.

Отрицанием называется  операция  получения  из  высказывания А такого  составного  высказывания   (читается  «не  А»),  которое истинно тогда, когда А ложно, и ложно тогда, когда А истинно.

• Использованию  операции  отрицания  в  русском  языке  соответствует употребление  частицы  «не»  перед  глаголом.  Например,  отрицанием  высказывания  А =  «Существует  наибольшее  простое  число» есть  высказывание А= «Не существует наибольшего простого числа».
• Высказывание  и  его  отрицание  не  могут  быть  одновременно  истинными или одновременно ложными.

Таблица  истинности операции отрицания имеет такой вид:

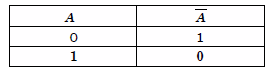
Конъюнкцией двух  высказываний  А и  В называется  операция получения  такого  составного  высказывания  А ^  В (читается  «А  и В»), которое  истинно  тогда  и  только  тогда,  когда  оба  высказывания А и В истинные.

• Использованию  операции  конъюнкции  в  русском  языке  соответствует употребление  союза  «и».  Например,  высказывание  В  =  «Число  27  кратно 3  и  число  27  кратно  9» является  конъюнкцией  двух  высказываний:  «Число 27 кратно 3» и «Число 27 кратно 9».
• Операцию конъюнкции также называют логическим умножением.
• По  определению,  конъюнкция  выполняется  над  двумя  высказываниями. Каждое  из  них  может  быть  либо  истинным,  либо  ложным.  Поэтому

  Таблица истинности операции конъюнкции имеет  такой вид:

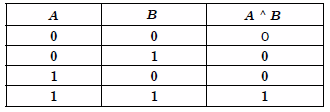
Дизъюнкцией двух  высказываний  А и  В  называется  операция получения  такого  составного  высказывания  A  v   В  (читается  «А или  В»),  которое  истинно  тогда  и  только  тогда,  когда  истинно  хотя бы одно из высказываний А или  В.

• Использованию  операции  дизъюнкции  в  русском  языке  соответствует употребление  союза  «или».  Например,  высказывание  С  =  «21  <  21»  является дизъюнкцией двух высказываний: «21 = 21» или «21 < 21».
• Операцию дизъюнкции также называют логическим сложением.
• По  определению,  дизъюнкция  выполняется  над  двумя  высказываниями.  Каждое  из  них  может  быть  либо  истинным,  либо  ложным.  Поэтому

Таблица истинности операции дизъюнкции имеет такой вид:

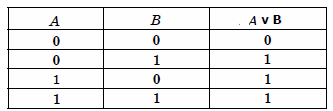
1. При  решении  многих  задач  встречаются  высказывания  с  переменными,  в  которых  используются  знаки  сравнения:  >  (больше),  <  (меньше), =  (равно),  <>  (не  равно),  >=  (больше  или  равно),  <=  (меньше  или  равно), например:  х > 5, у < z.
2. Такие высказывания могут быть истинными при одних значениях переменных и ложными при других.
3. Высказывание  х  <  0  является  простым,  а  высказывание  3  <  х  <  5  -составным.  Последнее  можно  представить  как  конъюнкцию  двух  простых высказываний: (х > 3) V (х < 5).

Логические переменные. Логические выражения и их таблицы истинности. Логические формулы

Алгеброй  логики  (булевой  логикой,  алгеброй  высказываний)  называют раздел  математической  логики,  в  котором  рассматриваются  общие  свойства  выражений,  составленных  из  высказываний с использованием логических операций.

В  алгебре  логики  используется  понятие  логическая переменная.

Логическая  переменная  — это  переменная,  которая  может  принимать только значения true или false.

Заданием  алгебры  логики  является  определение  истинности  логических выражений — выражений, которые состоят из логических констант, логических переменных, логических операций, скобок, например (A v B) a (A v   В).

1. Понятно,  что  значением  логического  выражения  может  быть  только true или false.
2. Для  логических  операций,  рассмотренных  выше,  определен  такой  приоритет  операций:  отрицание,  конъюнкция,  дизъюнкция.  Для  изменения этого порядка выполнения логических операций используют скобки.
3. Для  вычисления  значения  истинности  логического  выражения  можно использовать таблицы истинности.

Для построения и заполнения таблицы истинности нужно:

1. Вычислить  количество  возможных  наборов  значений  логических  переменных.  Если  выражение  содержит  n разных  логических  переменных,  то  возможных  наборов  значений  этих  переменных  будет  2^n.  Это число определяет количество строк в таблице истинности.

2. Определить  количество  логических  операций  в  логическом  выражении. Количество логических операций   плюс  количество  логических  переменных  определяет количество столбцов в таблице.

3. Заполнить первые n столбцов всеми возможными наборами значений логических переменных.

4. Заполнить каждый следующий столбец значениями, полученными - при выполнении очередной логической операции. Очередность устанавливается согласно названному приоритету операций.

В  последнем  столбце  таблицы  будут  получены  все  возможные  значения истинности заданного логического  выражения.

Пример.Определение истинности составного выражения Ā V (B Λ A) аналогично (not A) or (В and А):

1. Выражения содержит  две  логические  переменные, т.  е.  n =  2.  Следовательно,  всего  существует  4  набора  возможных  значений этих  переменных  (2n = 22 =  4).    2. Выражение  содержит  3  логические  операции:  отрицание,  дизъюнкция  и  конъюнкция.  Таким  образом,  таблица истинности  будет  состоять  из  4  строк  и  5  столбцов.   3.  Первой,  согласно  приоритету,  будет  выполняться  операция  отрицания,  второй  -  конъюнкции, последней  -  дизъюнкции,  в  которой  нужно  использовать  результаты первых двух операций.

Получим такую таблицу истинности:

Анализируя  последний  столбец  таблицы  истинности,  делаем  вывод,  что выражение  будет  иметь  значение  false только  в  случае,  когда  логические переменные  имеют  такие  значения:  А  =  true,  В =  false. Во  всех  остальных случаях значением логического выражения будет true.

Для  доказательства  этих  равносильностей  можно  составить  и  сравнить  таблицы  истинности  логических  выражений  в  правой  и  левой  частях.  Предлагаем  вам  сде­лать это самостоятельно.

Ветвление в алгоритмах и программах
Алгоритмы с ветвлением. Глобальные и локальные переменные 
Вложенные ветвления

• 2017 Февраль