Занятие 17. Основные понятия математической логики.

Для решения большинства задач линейных алгоритмов недостаточно.

В проектах, которые реализуют  другие виды алгоритмов, например алгоритмы с ветвлениями, используют логические выражения. Рассмотрим логические выражения и операции над ними.

1. Высказывания. Логические константы. Логические операции.

Логика - наука о формах, методах и законах интеллектуальной познавательной деятельности, правильного мышления, о способах рассуждений.

Математическая логика (один из разделов логики) - наука о законах математического мышления.

Высказывание (одно из основных понятий математической логики) - повествовательное предложение, о котором можно однозначно сказать, правильное (истинное) оно или неправильное (ложное) и обозначается большими буквами английского алфавита

Примеры:  А = "Киев - столица Украины", В="2+2=5".

Основное свойство высказывания - его истинность:

• 1 или true - если высказывание истинно       ( А = "Киев - столица Украины");
• 0 или false - если высказывание ложно.        (В="2+2=5").

Из заданных высказываний можно получать новые - составные, используя логические операции:

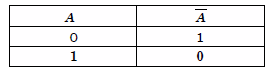
• отрицание - операция получения из высказывания А такого составного высказывания  "не А", которое истинно тогда, когда А ложно и наоборот.
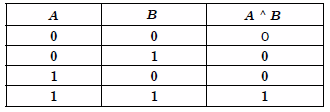
• конъюнкцию (объединение) - конъюнкцией двух высказываний А и В называется операция получения такого составного высказывания А^В ("читается А и В"), которое истинно тогда и только тогда, когда оба высказывания А и В истинны.Операцию конъюнкции также называют логическим умножением. ;
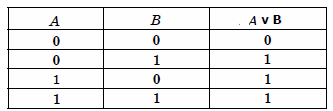
• дизъюнкцию (разъединение) -дизъюнкцией  двух высказываний А и В называется операция получения такого составного высказывания А^VВ ("читается А или В"), которое истинно тогда и только тогда, когда истинно хотя бы одно из   высказываний А или В .Операцию дизъюнкции  также называют логическим сложением.

Все эти операции возвращают результат булевого типа (boolean). 

Для определения результатов выполнения логических операций в математической логике используют таблицы истинности:

Таблица истинности операции отрицания	Таблица истинности операции конъюнкции	Таблица истинности операции дизъюнкции

При решении многих задач встречаются высказывания с переменными, в которых используются знаки сравнения: >(больше), < (меньше), = (равно), >= (больше или равно), <= (меньше или равно), <> (не равно).

  2.Логические переменные. Логические выражения и их таблицы истинности. Логические формулы. 

Алгеброй логики (булевой логикой, алгеброй высказываний) называют раздел математической логики, в котором рассматриваются  общие свойства выражений, составленных из высказываний с использованием логических операций.

В алгебре логики используется понятие Логическая переменная.

Логическая переменная - это переменная, которая может принимать только значение true  или false.

Приоритет рассмотренных логических операций: отрицание, конъюнкция, дизъюнкция.

Пример.Определение истинности составного выражения  (not A) or (В and А):

1.  Вычислить количество возможных наборов значений логических переменных А, В:

• количество логических переменных ⇒   n = 2;
• следовательно, количество возможных значений переменных 2ⁿ = 2² = 4.

2. Определить количество логических операций в логическом выражении ⇒ 3.

3. Количество  столбцов таблицы истинности это количество логических операций плюс количество логических переменных (2 + 3 = 5).

4. Заполнить первых n столбцов всеми возможными наборами значений переменных

5. Заполнить каждый следующий  столбец значениями, полученными при выполнении очередной логической операции. Очередность операций – по правилам приоритета:

1.операция логического отрицания;

2. операция конъюнкция – логическое умножение;

3. операция дизъюнкция – логическое сложение.

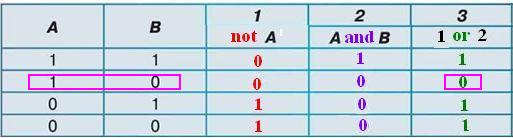
Анализируя последний столбец таблицы истинности, делаем вывод, что:

• выражение будет иметь значение false только в том случае, когда логические переменные имеют такие значения: A=true, B=false;
• во всех остальных случаях значением логического выражения будет true.

PS!!!

• Два логических выражения называются равносильными, если они принимают одинаковые значения при одних и тех же наборах значений логических переменных, которые входят в эти выражения.
• Равносильность двух логических выражений образует логическую формулу.

Приведем несколько интересных и полезных логических формул:

Для  доказательства  этих  равносильностей  можно  составить  и  сравнить  таблицы  истинности  логических  выражений  в  правой  и  левой  частях. 

3. Выполните задания.

занятие 18

• 2017 Февраль